How to do Iterative Postorder Traversal in BST
Earlier we have seen lot of tutorials related to Binary Search Tree like
How to find the diameter of a binary tree
Converting a Binary Tree into its Mirror Tree
Inorder Predecessor and Successor of Binary Search Tree
How to find all leaf nodes in Binary Search Tree
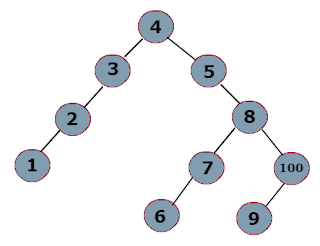
In this tutorial we will see how to do postorder traversal using iterative method instead of recrusive algorithm. We are going to use single stack to store nodes and applying our logic over it to get postorder traversal.
Simple Java code to create Binary Search Tree and doing postorder traversal using iterative method.
OUTPUT:
How to find the diameter of a binary tree
Converting a Binary Tree into its Mirror Tree
Inorder Predecessor and Successor of Binary Search Tree
How to find all leaf nodes in Binary Search Tree
In this tutorial we will see how to do postorder traversal using iterative method instead of recrusive algorithm. We are going to use single stack to store nodes and applying our logic over it to get postorder traversal.
Simple Java code to create Binary Search Tree and doing postorder traversal using iterative method.
import java.util.Stack; class Node { Node left, right; int data; public Node(int data) { this.data = data; } } public class PostOrderTraversal { public static void main(String[] args) { int a[] = { 4, 5, 8, 100, 3, 2, 9, 1, 7, 6 }; Node root = null; PostOrderTraversal tree = new PostOrderTraversal(); for (int i = 0; i < a.length; i++) { root = tree.insertNode(root, a[i]); } System.out.println("\n\nBy Stack : "); tree.postOrderTraversal(root); } /* * Postorder traversal using iteration and single stack */ public void postOrderTraversal(Node root) { //Stack to store each node Stack<Node> stack = new Stack<Node>(); //Strong all left node from root into stack while (root != null) { stack.push(root); root = root.left; } Node node = null; while (stack.size() > 0) { // Boolean flag to check left and right nodes are visited or not boolean leftVisited = false, rightVisited = false; // Checking whether current node is equal to roots left node (1) if (node != null && stack.peek().left == node) { leftVisited = true; // Checking whether current node is equal to roots right node (2) } else if (node != null && stack.peek().right == node) { leftVisited = rightVisited = true; } node = stack.peek(); // if above check (1) fails then push current nodes left node into stack if (node.left != null && !leftVisited) { stack.push(node.left); // if above check (2) fails then push current nodes right node into stack } else if (node.right != null && !rightVisited) { stack.push(node.right); } else { node = stack.pop(); System.out.print(node.data + ", "); } } } public Node insertNode(Node root, int data) { Node currentNode = new Node(data); if (root == null) { root = currentNode; } else { insertData(currentNode, root); } return root; } public Node insertData(Node newNode, Node root) { if (root.data < newNode.data) { if (root.right == null) { root.right = newNode; } else { return insertData(newNode, root.right); } } else if (root.data > newNode.data) { if (root.left == null) { root.left = newNode; } else { return insertData(newNode, root.left); } } return root; } }
OUTPUT:
By Stack : 1, 2, 3, 6, 7, 9, 100, 8, 5, 4,

