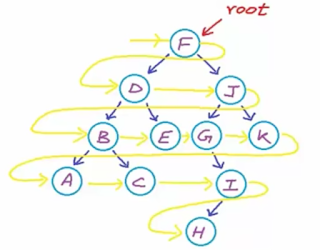
How to create a graph using Java
Let's see simple graph creation using core java and printing all the vertex along with list of edges which goes from that particular Vertex.
OUTPUT:
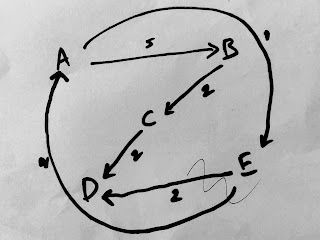
public class MyGraph { public static void main(String[] args) { /* Initilize graph with 5 vertex and as * going to be directed graph */ Graph myGra = new Graph(5, "directed"); /* * Add vertex */ myGra.addVertex("A"); myGra.addVertex("B"); myGra.addVertex("C"); myGra.addVertex("D"); myGra.addVertex("E"); /* * Add edges between each vertex and their distance */ myGra.addEdge("A", "B",5); myGra.addEdge("A", "E",1); myGra.addEdge("B", "C",2); myGra.addEdge("C", "D",2); myGra.addEdge("E", "D",2); myGra.addEdge("E", "A",2); // Print the created graph myGra.printMyGraph(); } }
public class Graph { // Graph direction (directed / undirected graph) private boolean undirected = true; // No. of vertex in the graph private Vertex[] arrayOfVertex; private int indexCounter = 0; // Constructor to create graph vertex public Graph(int noOfVertex, String graphType) { if (graphType.equalsIgnoreCase("directed")) { this.undirected = false; } arrayOfVertex = new Vertex[noOfVertex]; } // Vertex class class Vertex { // Name of the Vertex private String name; // Holds the list of all edges from current vertex private Edge edge; // Create vertex public Vertex(String name, Edge aNode) { this.name = name; this.edge = aNode; } } // Edge between 2 Vertex class Edge { // Destination vertex Id private int vertexId; // In list point to next edge if its else null private Edge next; // Weight of current edge private int weight; // Create edge public Edge(int vertexId, Edge next, int weight) { this.vertexId = vertexId; this.next = next; this.weight = weight; } } // Adding Vertex public void addVertex(String vertexName) { arrayOfVertex[indexCounter] = new Vertex(vertexName, null); indexCounter++; } // Adding Edge public void addEdge(String sVertex, String dVertex, int weight) { int sId = indexOfName(sVertex); int dId = indexOfName(dVertex); /* * Find source and destination vertexId and create new Edge and * point it to source edge link */ arrayOfVertex[sId].edge = new Edge(dId, arrayOfVertex[sId].edge, weight); /* * If undirected then create 2 edge's between source and destination and * destination to source */ if (undirected) { arrayOfVertex[dId].edge = new Edge(sId, arrayOfVertex[dId].edge, weight); } } /* * Getting indexId of given vertex name */ private int indexOfName(String name) { for (int v = 0; v < arrayOfVertex.length; v++) { if (arrayOfVertex[v].name.equals(name)) { return v; } } return -1; } /* * Print the graph in vertex order and listing all outgoing edges from that vertex */ public void printMyGraph() { System.out.println("VERTEX\t----> EDGES WITH WEIGHT"); for (int v = 0; v < arrayOfVertex.length; v++) { System.out.print(arrayOfVertex[v].name +" \t ----> "); for (Edge aNode = arrayOfVertex[v].edge; aNode != null; aNode = aNode.next) { System.out.print( "<==>"+ arrayOfVertex[aNode.vertexId].name + ":" + aNode.weight); } System.out.println(); } } }
OUTPUT:
VERTEX ----> EDGES WITH WEIGHT A ----> <==>E:1<==>B:5 B ----> <==>C:2 C ----> <==>D:2 D ----> E ----> <==>A:2<==>D:2