Counting nodes in a tree? Yes how to get Binary Tree size
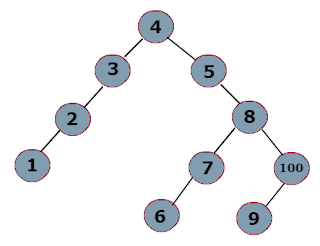
Counting nodes in a tree? Yes how to get Binary Tree size nothing but counting all the nodes in a Binary Tree. For example the size of the below binary tree is 11 Lets...
Showing posts with label Algorithm. Show all posts
Showing posts with label Algorithm. Show all posts
How to do Iterative Postorder Traversal in BST
Earlier we have seen lot of tutorials related to Binary Search Tree like How to find the diameter of a binary tree Converting a Binary Tree into its Mirror Tree Inorder Predecessor and Successor...
How to write a simple and easy Binary search algorithm
Given a sorted array array[] of n elements and need to find the element 'val' present in the array or not by using Binary search technique. NOTE: Binary search works only on sorted array....
Cool !!! How to find the diameter of a binary tree
Given a binary tree, you need to compute the length of the diameter of the tree. The diameter of a binary tree is the length of the longest path between any two nodes in a tree....
Know How to find all leaf nodes in binary tree
Create a Binary Tree with from the given array of values and then find all the leaf nodes from left to right. Leaf nodes are nothing but bottom/last nodes with both left and right...
Longest Common Subsequence (LCS) algorithm using Dynamic Programming in java
The Longest Common Subsequence (LCS) problem is given with two strings like "ABAZDC" and "BACBAD". LCS is to find their longest common subsequence that appear left-to-right but not necessarily in a contiguous block in...
