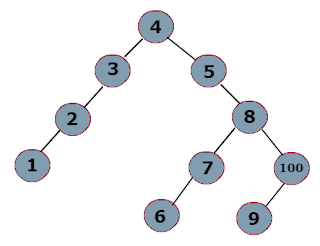
Simple, how to get only left child in BST
As same as traversals like inorder, preorder, postorder and level order we need to traverse to BST and need to print only the left child of each nodes in Binary Search Tree.
From below example we need to get only the nodes including root nodlike 11, 6, 4, 17, 31
Solution:
From below example we need to get only the nodes including root nodlike 11, 6, 4, 17, 31
Solution:
- Place the root node in Queue.
- Iterate Queue until queue becomes empty.
- Next Enqueue the child nodes left and right nodes inside same queue and print only the left node values.
- Repeat the process for each leaf node.
class Node {
Node left, right;
int data;
public Node(int data) {
this.data = data;
}
}
public class LeftNodes {
public static void main(String[] args) {
int a[] = { 4, 5, 3, 8, 7, 6, 100, 9, 3, 2, 1 };
Node root = null;
LeftNodes tree = new LeftNodes();
for (int i = 0; i < a.length; i++) {
root = tree.insertNode(root, a[i]);
}
tree.printLeftNodes(root);
}
public void printLeftNodes(Node root) {
if (root == null)
return;
Queue<Node> queue = new LinkedList<Node>();
queue.add(root);
System.out.println(root.data);
while (queue.size() > 0) {
Node current = queue.poll();
if (current.left != null) {
System.out.println(current.left.data);
queue.add(current.left);
}
if (current.right != null) {
queue.add(current.right);
}
}
}
public Node insertNode(Node root, int data) {
Node currentNode = new Node(data);
if (root == null) {
root = currentNode;
} else {
insertData(currentNode, root);
}
return root;
}
public Node insertData(Node newNode, Node root) {
if (root.data < newNode.data) {
if (root.right == null) {
root.right = newNode;
} else {
return insertData(newNode, root.right);
}
} else if (root.data > newNode.data) {
if (root.left == null) {
root.left = newNode;
} else {
return insertData(newNode, root.left);
}
}
return root;
}
}
OUTPUT:
4
3
2
1
7
6
9